tetraedr+sphere

where 19,5º comes from? let's find out.

let us assume we have a tetraedr with all side of length 'a'.

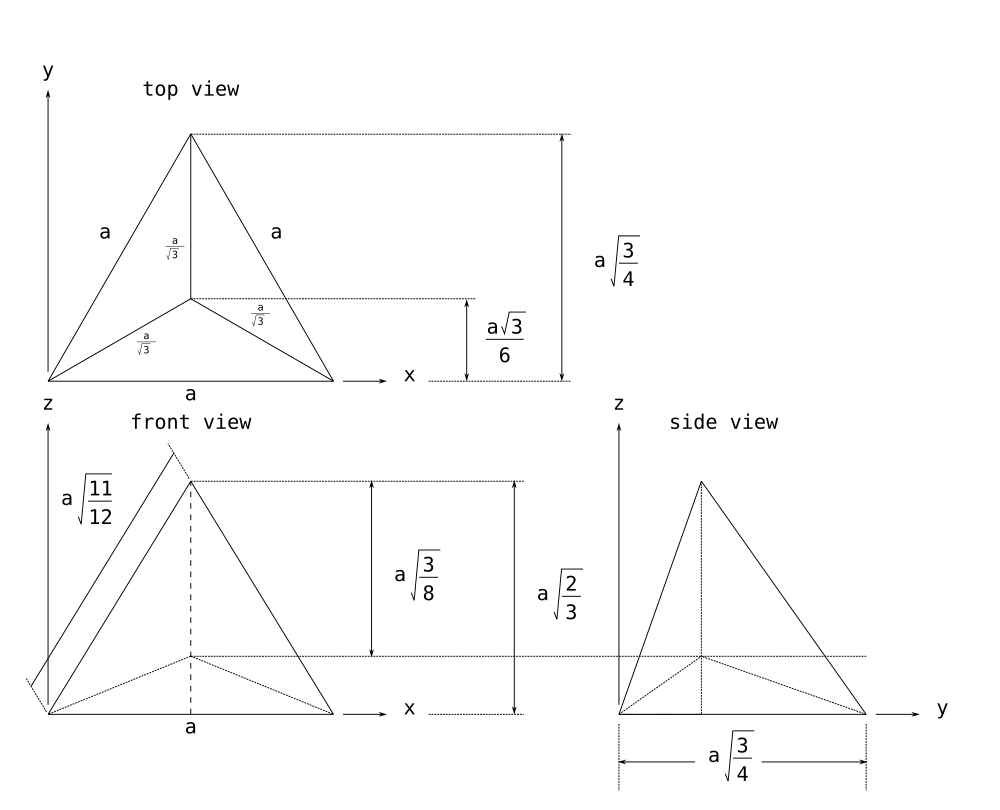
the angle between the edge and middle point on top view of the tetraedr is 30º. tangent of an angle equals to opposite divided by adjacent. let opposite be 'c', and adjacent is a/2, then:

$$\tan {30}^{\circ }=\frac{c}{a/2}$$

$$\frac{\sqrt{3}}{3}=\frac{c}{a/2}$$

$$c=\frac{a\sqrt{3}}{6}$$

now let's calculate the length between the edge and middle point on top view. we use pifagor's theorem:

$$\sqrt{{\left(\frac{a}{2}\right)}^2+{\left(\frac{a\sqrt{3}}{6}\right)}^2}=\sqrt{\frac{a^2}{4}+\frac{3a^2}{36}}=$$

$$=\sqrt{\frac{9a^2+3a^2}{36}}=\frac{a\sqrt{12}}{6}=\frac{a}{\sqrt{3}}$$

we will also need to know the height of the triangle in top view:

$$\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\sqrt{a^2-\frac{a^2}{4}}=\sqrt{\frac{4a^2-a^2}{4}}=a\sqrt{\frac{3}{4}}$$

now, using an equation of lenght of a 3D line, we calculate the distance between edge and middle point of the tetraedr in 3D:

$$h=\sqrt{{\left(\frac{a}{2}\right)}^2+{\left(\frac{a\sqrt{3}}{6}\right)}^2+{(a\sqrt{\frac{2}{3}}-h)}^2}$$

$$h=\sqrt{\frac{a^2}{4}+\frac{3a^2}{36}+\frac{2}{3}{a}^2-2\sqrt{\frac{2}{3}}ah+h^2}$$

$$h^2=a^2-2\sqrt{\frac{2}{3}}ah+h^2$$

$$2\sqrt{\frac{2}{3}}ah=a^2$$

$$h=\frac{1}{2}\sqrt{\frac{3}{2}}a=\sqrt{\frac{3}{8}}a$$

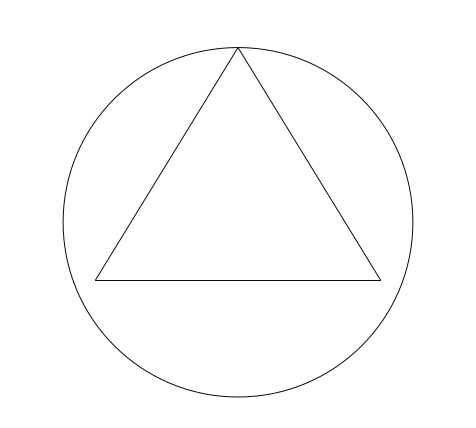
now, if we put the tetraedr inside a sphere, the angle between the equator and a point where tetraedr touches the sphere is:

$$\alpha =\arcsin \frac{\sqrt{\frac{2}{3}}-\sqrt{\frac{3}{8}}}{\sqrt{\frac{3}{8}}}=\arcsin \left(\frac{1}{3}\right)\approx 19,{47122}^{\circ }$$